Problem des Monats Dezember

Eva ist Mathematikerin. Sie möchte an ihrem Adventskranz jeden Sonntag die Kerzen eine Stunde lang anzünden, natürlich am ersten Adventssonntag nur eine Kerze, am zweiten zwei Kerzen usw. Außerdem möchte sie, dass nach dem vierten Adventssonntag alle Kerzen gleich weit heruntergebrannt sind. Wie kann sie das schaffen? Selbstverständlich waren alle Kerzen gleich lang, als Eva den Adventskranz kaufte. Sie schneidet auch keine Stücke von den Kerzen ab.

Lösung:

Die gesamte Brennzeit der Kerzen beträgt 1 + 2 + 3 + 4 = 10 Stunden. Verteilt auf 4 Kerzen muss somit während der Adventszeit jede Kerze 2,5 Stunden brennen. Das geht nur dann, wenn an wenigstens einem Sonntag zwischendurch Kerzen ausgemacht und dafür andere angezündet werden.
Eine mögliche Lösung ist:

	Kerze 1	Kerze 2	Kerze 3	Kerze 4
Sonntag 1	1 Stunde
Sonntag 2	0,5 Stunden	0,5 Stunden	0,5 Stunden	0,5 Stunden
Sonntag 3		1 Stunde	1 Stunde	1 Stunde
Sonntag 4	1 Stunde	1 Stunde	1 Stunde	1 Stunde

2. Aufgrund der schlechten Wirtschaftslage fordern die Händler die Verlängerung der Adventszeit auf 5 Wochen. Die Adventskränze werden dann natürlich 5 Kerzen haben müssen. Eva aus der ersten Aufgabe ist übrigens auch sehr dafür, denn bei einem solchen Adventskranz wird es für sie einfacher, dass am Ende alle Kerzen gleich weit abgebrannt sind.
   Untersuche, warum das für sie einfacher wird.
   Wie wird es sein, wenn es sogar eine Verlängerung auf 6 Wochen geben sollte?

Lösung

Bei 5 Wochen beträgt die gesamte Brennzeit 15 Stunden, das bedeutet, jede Kerze muss 3 Stunden lang brennen. Deshalb gibt es Lösungen, bei denen nicht zwischendurch Kerzen gelöscht werden müssen.
Eine mögliche Lösung ist:

	Kerze 1	Kerze 2	Kerze 3	Kerze 4	Kerze 5
Sonntag 1	1 Stunde
Sonntag 2	1 Stunde	1 Stunde
Sonntag 3			1 Stunde	1 Stunde	1 Stunde
Sonntag 4		1 Stunde	1 Stunde	1 Stunde	1 Stunde
Sonntag 5	1 Stunde	1 Stunde	1 Stunde	1 Stunde	1 Stunde

Bei 6 Wochen ist die gesamte Brennzeit 21 Stunden, jede Kerze muss 3,5 Stunden lang brennen. Damit wird es wieder schwieriger.

Im Wohnzimmer von Evas Familie stehen 5 Kerzen so verteilt, wie in der Abbildung dargestellt. Sie möchte alle Kerzen anzünden. Da sie sehr sparsam ist, will sie möglichst mit einem Streichholz auskommen und sucht deshalb den kürzesten Weg, auf dem sie alle Kerzen erreichen kann. Zwischen den Kerzen stehen keine Einrichtungsgegenstände wie Stühle oder Tische herum. Die hat Eva vorher beiseite geräumt. Kannst Du bei der Suche nach dem kürzesten Weg helfen?

Lösung:

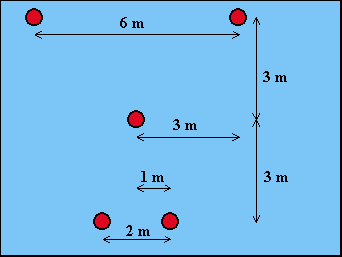
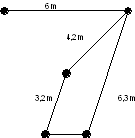
Die Kerzen werden in ein Bild gezeichnet, so dass 1 m durch  1 cm dargestellt wird. Dann können die Abstände zwischen je zwei Kerzen gemessen werden:

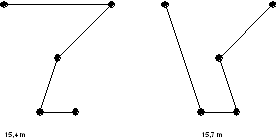
Probiert man nun alle Wege aus, findet man zwei besonders kurze Wege.

Der links dargestellte Weg ist noch ein bisschen kürzer.