Regelheft
Schuljahr 2002/2003

1. Brüche bestehen aus einem Zähler, der auf dem Bruchstrich steht, und einem Nenner, der unter dem Bruchstrich steht.

2. Auch Brüche sind als Punkte auf dem Zahlenstrahl darstellbar; Brüche, die zum selben Punkt gehören, haben den selben Wert. Diesen Wert nennt man Bruchzahl.

3. Die Menge der Bruchzahlen wird als 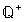 bezeichnet.

4. Brüche mit dem Zähler 1 heißen Stammbrüche, Brüche, deren Zähler kleiner als der Nenner sind, bezeichnet man als echte Brüche.

5. Brüche, deren Zähler größer als der Nenner sind, nennt man unechte Brüche.

6. Brüche, deren Zähler ein Vielfaches des Nenners ist, heißen Scheinbrüche.

7. Jedem Quotienten 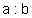 entspricht der Bruch 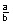; dabei darf der Nenner nicht Null sein.

8. Zu jeder Gleichung der Form 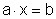 gibt es in 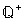 eine Lösung .

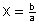9. Ein Bruch ändert seinen Wert nicht, wenn man Zähler und Nenner mit der gleichen natürlichen Zahl multipliziert; diesen Vorgang nennt man Erweitern.

10. Ein Bruch ändert seinen Wert nicht, wenn man Zähler und Nenner durch die gleiche natürliche Zahl dividiert; diesen Vorgang nennt man Kürzen.

11. Von zwei Brüchen mit dem gleichen Nenner ist derjenige der größere, der den größeren Zähler hat.

12. Von zwei Brüchen mit dem gleichen Zähler ist derjenige der größere, der den kleineren Nenner hat.

13. Brüche mit verschiedenen Nennern müssen vor dem Größenvergleich auf einen gemeinsamen Nenner erweitert werden.

14. Der Hauptnenner ist der kleinste gemeinsame Nenner mehrerer Brüche; er ist das kgV der gegebenen Nenner.

15. Brüche mit gleichem Nenner werden addiert, indem man die Zähler addiert und den Nenner beibehält.

16. Brüche mit gleichem Nenner werden subtrahiert, indem man die Zähler subtrahiert und den Nenner beibehält.

17. Brüche mit verschiedenen Nennern müssen vor dem Addieren bzw. dem Subtrahieren auf den gleichen Nenner, am besten den Hauptnenner, gebracht werden.

18. Zahlen, die aus natürlichen Zahlen und Brüchen bestehen, heißen gemischte Zahlen.

19. Gemischte Zahlen werden in einen unechten Bruch umgewandelt, indem man die natürliche Zahl mit dem Nenner multipliziert und den Zähler addiert. Dies ergibt den neuen Zähler, während der Nenner beibehalten wird.

20. Ein unechter Bruch wird in eine gemischte Zahl umgewandelt, indem man den Zähler durch den Nenner dividiert. Die Ganzen bilden die natürliche Zahl; der Rest, der sich beim Teilen ergibt, wird der neue Zähler, während der Nenner beibehalten wird.

21. Gemischte Zahlen werden addiert bzw. subtrahiert, indem man sie zunächst in unechte Brüche umwandelt, diese dann addiert bzw. subtrahiert und schließlich das Ergebnis wieder in eine gemischte Zahl umwandelt.

22. Brüche werden multipliziert, indem man die Zähler und die Nenner jeweils miteinander multipliziert.

23. Beim Multiplizieren müssen gemischte Zahlen zuerst in Brüche umgewandelt werden.

24. Vertauscht man Zähler und Nenner eines Bruches, so erhält man seinen Kehrbruch.

25. Durch einen Bruch wird dividiert, indem man mit seinem Kehrbruch multipliziert.

26. Der Wert eines Dezimalbruches bleibt unverändert, wenn man Endnullen anhängt (erweitert) oder Endnullen weglässt.

27. Beim Vergleich von Dezimalbrüchen geht man folgendermaßen vor:

    a)       Man multipliziert die zu vergleichenden Dezimalbrüche mit der gleichen Stufenzahl so, dass jeweils eine natürliche Zahl entsteht.

b)       Je kleiner die dabei entstehende natürliche Zahl ist, desto kleiner ist der zugehörige Dezimalbruch.

28. Ein Intervall ist die Menge aller Zahlen zwischen zwei Grenzzahlen.

29. In einem abgeschlossenen Intervall gehören die beiden Grenzzahlen zum Intervall, in einem halboffenen nur eine der Grenzzahlen, in einem offenen keine der beiden Grenzzahlen.

30. Intervallschreibweisen:

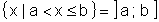
31. Mathematische Rundungsregel: Ist die erste der weggelassene Ziffern kleiner als 5, so wird abgerundet, sonst aufgerundet.

32. Bei gerundeten Dezimalbrüchen dürfen weder Nullen angehängt noch Endnullen weggelassen werden.

33. Eine gerundete Zahl vertritt ein halboffenes Intervall, bei dem die niedrigere Grenzzahl dazugehört.

34. Dezimalbrüche werden addiert bzw. subtrahiert, in dem man (wie bei den natürlichen Zahlen) die Ziffern mit dem gleichen Stellenwert addiert bzw. subtrahiert.

35. Ein Dezimalbruch wird mit einer Stufenzahl multipliziert, indem man das Komma um so viele Stellen nach rechts rückt, wie die Stufenzahl Nullen hat.

36. Ein Dezimalbruch wird durch eine Stufenzahl dividiert, indem man das Komma um so viele Stellen nach links rückt, wie die Stufenzahl Nullen hat.

37. Zwei Dezimalbrüche werden miteinander multipliziert, indem man zunächst die beiden Zahlen ohne Berücksichtigung der Kommas multipliziert; beim Ergebnis setzt man das Komma so, dass es so viele Dezimalstellen hat wie die beiden Faktoren zusammen hatten.

38. Der Wert eines Quotienten ändert sich nicht, wenn man Dividend und Divisor mit derselben Zahl multipliziert.

39. Bei der Division zweier Dezimalbrüche schiebt man beide Kommas um so viele Stellen nach rechts, bis der Divisor eine natürliche Zahl ist. Überschreitet man bei der Division das Komma im Dividend, muss man im Ergebnis das Komma setzen.

40. Enthält der Nenner eines gewöhnlichen Bruches nur die Primfaktoren 2 und/oder 5, so lässt sich dieser Bruch in einen endlichen Dezimalbruch umwandeln.

41. Enthält der Nenner eines gewöhnlichen Bruches weder den Primfaktor 2 noch den Primfaktor 5, so lässt sich dieser Bruch nur in einen unendlichen, reinperiodischen Dezimalbruch umwandeln (durch eine Division).

42. Enthält der Nenner eines gewöhnlichen Bruches neben anderen Primfaktoren auch den Primfaktor 2 oder den Primfaktor 5, so lässt sich dieser Bruch nur in einen unendlichen, gemischt-periodischen Dezimalbruch umwandeln (durch eine Division).

43. Man erhält den Mittelwert (Durchschnitt), indem man den Wert der Summe durch die Anzahl der Summanden dividiert.

44. Zwei Halbgeraden mit einem gemeinsamen Anfangspunkt (Scheitelpunkt) bilden einen Winkel. Die beiden Halbgeraden, die einen Winkel einschließen, nennt man Schenkel. Dabei beschreibt ein Winkel eine Drehung, in der Regel gegen den Uhrzeigersinn.

45. Die Größe der Winkel wird in Grad angegeben (1°). Eine Volldrehung entspricht einem Winkel von 360°.

46. Spitz nennt man einen Winkel, der kleiner als 90° ist; ein rechter Winkel hat eine Größe von 90°, ein gestreckter eine von 180°. Einen Winkel, der größer als 90°, aber kleiner als 180° ist, nennt man stumpf, einen, der zwischen 180° und 360° liegt, überstumpf.

47. Einen Winkel beschreibt man durch die beiden Schenkel bzw. durch 3 Punkte. Dabei wird stets der Scheitel in der Mitte angegeben. Der Punkt auf dem ersten Schenkel wird zuerst genannt.

48. Das Volumen (=Rauminhalt) eines Würfels mit der Kantenlänge 1 dm ist 1 dm³ (Kubikdezimeter).

49. Der Rauminhalt eines Quaders ist das Produkt der Grundfläche mit der Höhe.

50. Die Umrechnungszahl bei Volumeneinheiten beträgt 1000.

51. Als Hohlmaße bezeichnet man die Einheiten Hektoliter (hl), Liter (l) und Milliliter (ml). Dabei sind 100 l 1 hl.

52. Unter der absoluten Häufigkeit versteht man die Anzahl der Ergebnisse eines Experimentes; unter der relativen Häufigkeit versteht man den Quotienten aus der Anzahl der gesuchten Ergebnisse und der Gesamtzahl der Ergebnisse.

53. Den Zähler eines Bruches mit dem Nenner 100 bezeichnet man als Prozentsatz.

54. Der Prozentsatz vom Grundwert ist der Prozentwert.

55. Prozentsätze können nur verglichen werden, wenn sie auf den gleichen Grundwert bezogen sind!

56. Bruttogewicht (100%) minus Tara ist Nettogewicht.

57. Bruttolohn (100%) minus Abzüge ist Nettolohn.

58. Rabatt ist ein Preisnachlass, den der Händler gewährt; er wird vor Berechnung der Mehrwertsteuer ermittelt.

59. Die Mehrwertsteuer ist ein Preisaufschlag, der an den Staat abgeführt werden muss.

60. Skonto ist ein Preisnachlass, der bei Bezahlung innerhalb einer bestimmten Frist gewährt wird; Skonto wird nach der Berechnung der Mehrwertsteuer ermittelt.

61. Größen heißen direkt proportional, wenn die Zahlenpaare den gleichen Quotienten haben. Direkt proportionale Größen erkennt man daran, dass zum halben, doppelten, dreifachen, ... Wert bzw. zum dritten, vierten,  .... Teil der einen Größe der halbe, doppelte, dreifache, ... Wert bzw. der dritte, vierte, .... Teil der anderen Größe gehört.

62. Größen heißen indirekt proportional, wenn Zahlenpaare den gleichen Produktwert haben. Indirekt proportionale Größen erkennt man daran, dass zum doppelten, dreifachen, vierfachen, ... Wert der einen Größe die Hälfte bzw. der dritte, vierte, .... Teil der anderen Größe gehört.