Archiv der Knobelaufgaben

Aufgabe 1 (Dezember 2001):

Professor Wurzel ist Mathematiker und ein Sonderling. Er möchte an seinem Adventskranz jeden Sonntag die Kerzen eine Stunde lang anzünden, natürlich am ersten Adventssonntag nur eine Kerze, am zweiten zwei Kerzen usw. Außerdem möchte er, dass nach dem vierten Adventssonntag alle Kerzen gleich weit heruntergebrannt sind. Wie kann er das schaffen? Selbstverständlich waren alle Kerzen gleich lang, als der Professor den Adventskranz kaufte. Er schneidet auch keine Stücke von den Kerzen ab.

Schon seit Monaten gibt es in den Geschäften Lebkuchen, Weihnachtsmänner aus Schokolade, Christstollen. Jetzt fordern die Händler auch noch die Verlängerung der Adventszeit auf 5 Wochen. Die Adventskränze werden dann natürlich 5 Kerzen haben müssen. Professor Wurzel aus der ersten Knobel-Aufgabe ist übrigens auch sehr dafür, denn bei einem solchen Adventskranz wird es für ihn einfacher, dass am Ende alle Kerzen gleich weit abgebrannt sind.
Untersuche, warum das für ihn einfacher wird.
Wie wird es sein, wenn es sogar eine Verlängerung auf 6 Wochen geben sollte?

Aufgabe 3 (Januar 2002):

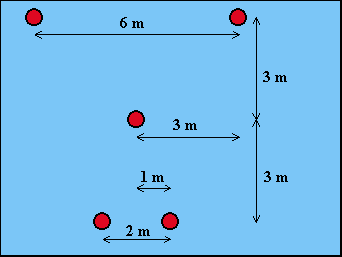Im Wohnzimmer von Professor Wurzel stehen 5 Kerzen so verteilt, wie in der Abbildung dargestellt. Der Professor möchte sie alle anzünden. Da er nicht nur ein Sonderling, sondern auch noch sehr sparsam ist, will er möglichst mit einem Streichholz auskommen und sucht deshalb den kürzesten Weg, auf dem er alle Kerzen erreichen kann. Zwischen den Kerzen stehen keine Einrichtungsgegenstände wie Stühle oder Tische herum. Die hat Professor Wurzel vorher beiseite geräumt. Kannst Du bei der Suche nach dem kürzesten Weg helfen?

Knobelaufgabe 3 (Februar 2002)

1. Wie kann man mit einem 6-l-Eimer und einem 10-l-Eimer aus einer genügend großen Regenwassertonne durch geschicktes Umfüllen 2 l Wasser abmessen?
   
2. Gesucht ist die größte sechsstellige Zahl, für die folgendes gilt:
   1. Die Zahl ist gerade.
   2. Die Zehnerziffer stellt eine dreimal so große Zahl dar wie die Zehntausenderziffer.
   3. Die Einer- und die Tausenderziffer kann man vertauschen, ohne dass sich die sechsstellige Zahl ändert.
   4. Die Hunderterziffer stellt eine halb so große Zahl dar wie die Hunderttausenderziffer.
      
3. Für die Buchstaben sind die Grundziffern ( 0,1,2,...,8,9) so einzutragen, dass für gleiche Buchstaben gleiche Grundziffern und für unterschiedliche Buchstaben verschiedene Grundziffern stehen und dass die angegebenen Rechenoperationen richtig gelöst sind.

   A	*	A	=	B
   *		-		-
   C	*	C	=	D
   --	--	--	--	--
   E	-	F	=	G